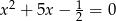Zadanie nr 9883769
Ułóż równanie kwadratowe, takie, by suma pierwiastków równania była równa 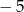 oraz by suma odwrotności jego pierwiastków była równa 10.
oraz by suma odwrotności jego pierwiastków była równa 10.
Rozwiązanie
Wyliczymy wartości wyrażeń 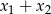 i
i 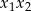 , które na mocy wzorów Viète’a dają współczynniki
, które na mocy wzorów Viète’a dają współczynniki 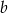 i
i  równania
równania
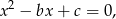
którego rozwiązaniami są 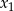 i
i 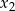 .
.
Mamy 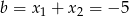 oraz
oraz
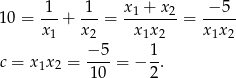
Zatem szukane równanie to 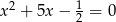 .
.
Powyżej znaleźliśmy przykład równania, o żądanych własnościach. Gdybyśmy chcieli wyznaczyć wszystkie takie równania, to musimy odpowiedź przemnożyć przez dowolne 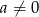 (bo ta operacja nie zmienia pierwiastków równania).
(bo ta operacja nie zmienia pierwiastków równania).
Odpowiedź: