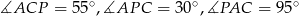Zadanie nr 4590175
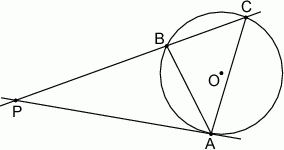
Z punktu  poprowadzono styczną do okręgu o środku
poprowadzono styczną do okręgu o środku  w punkcie
w punkcie  oraz sieczną, która ma z tym okręgiem dwa punkty wspólne
oraz sieczną, która ma z tym okręgiem dwa punkty wspólne 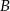 oraz
oraz 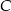 . Wiadomo, że
. Wiadomo, że 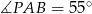 oraz
oraz 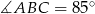 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta  .
.
Rozwiązanie
Obliczmy najpierw miarę kąta  .
.
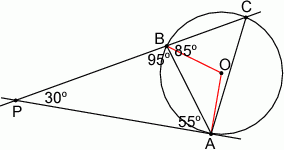
Patrzymy na trójkąt 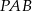 .
.
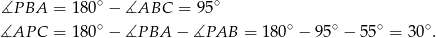
Sposób I
Korzystamy z twierdzenia o stycznej i siecznej. Mamy zatem
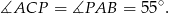
Stąd
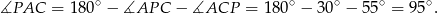
Sposób II
Dorysujmy promienie 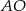 i
i 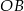 . Promień
. Promień 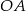 jest prostopadły do stycznej
jest prostopadły do stycznej 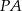 , więc
, więc
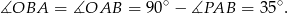
Stąd
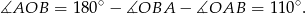
Na mocy twierdzenia o kątach wpisanym i środkowym mamy
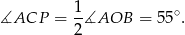
Stąd
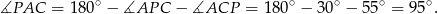
Odpowiedź: