/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Styczność/Różne

Zadanie nr 8450741

Z punktu 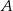A leżącego na okręgu poprowadzono średnicę 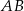AB i cięciwę 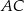AC , które tworzą kąt o mierze 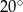20∘ . Przez punkt 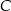C poprowadzono styczną do okręgu przecinającą prostą 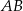AB w punkcie 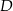D . Oblicz miary pozostałych kątów trójkąta ACD .

Wersja PDF

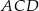Rozwiązanie

Zaczynamy od rysunku.

PIC

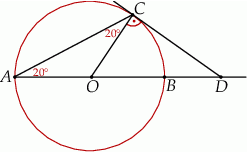
Ponieważ trójkąt 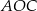AOC jest równoramienny, więc

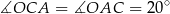
∡OCA = ∡OAC = 2 0∘

Ponieważ styczna jest prostopadła do promienia 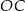OC mamy

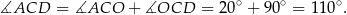
∘ ∘ ∘ ∡ACD = ∡ACO + ∡OCD = 20 + 90 = 110 .

Zatem

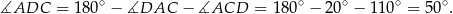
∘ ∘ ∘ ∘ ∘ ∡ADC = 180 − ∡DAC − ∡ACD = 18 0 − 20 − 110 = 50 .

 
Odpowiedź: 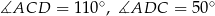∡ACD = 11 0∘, ∡ADC = 50∘ .

Wersja PDF