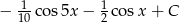/Studia/Analiza/Całki nieoznaczone/Trygonometryczne/Bez ułamka

Zadanie nr 9145227

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę 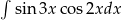∫ sin 3x cos2xdx .

Rozwiązanie

Sposób I

Aby zamienić iloczyn w całkowanej funkcji na sumę, skorzystamy ze wzoru

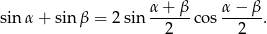
α-+-β- α-−-β- sin α + sinβ = 2 sin 2 cos 2 .

Aby prawa strona tego wzoru wyglądała jak całkowana funkcja musimy mieć

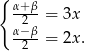
{ α+β-= 3x α2−β -2--= 2x.

Dodając te równania stronami mamy 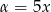α = 5x , a odejmując 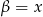β = x . Zatem

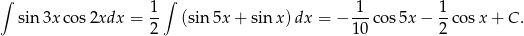
∫ ∫ 1- -1- 1- sin 3x cos2xdx = 2 (sin5x + sin x)dx = − 10 cos 5x − 2 cos x+ C.

Sposób II

Liczymy dokładnie tak samo jak poprzednio, ale korzystamy z gotowego wzoru

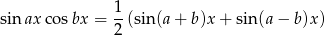
1 sin ax cosbx = --(sin(a+ b)x + sin(a− b)x) 2

Mamy więc

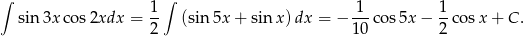
∫ 1∫ 1 1 sin 3x cos2xdx = -- (sin5x + sin x)dx = − ---cos 5x − --cos x+ C. 2 10 2

 
Odpowiedź: − 110 cos5x − 12 cos x+ C

Wersja PDF