/Konkursy/Zadania/Równania/Układy równań

Zadanie nr 8732120

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz w zależności od parametru a liczbę rozwiązań układu równań

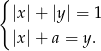
{ |x |+ |y| = 1 |x |+ a = y .

Rozwiązanie

Sposób I

Odejmując od pierwszego równania drugie (żeby skrócić 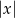|x| ) mamy

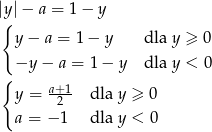
|y|− a = 1 − y { y− a = 1− y dla y ≥ 0 −y − a = 1− y dla y < 0 { a+1- y = 2 dla y ≥ 0 a = − 1 dla y < 0

Jeżeli 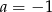a = − 1 to dowolny 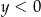y < 0 spełnia powyższy warunek i z równości 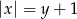|x| = y + 1 widać, że takie 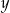y -ki dają nieskończenie wiele rozwiązań układu. Załóżmy dalej, że 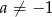a ⁄= − 1 . Zatem 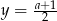y = a+1- 2 o ile

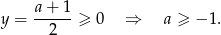
a-+-1- y = 2 ≥ 0 ⇒ a ≥ − 1.

Mam ponadto 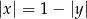|x | = 1− |y| . To równanie będzie miało jedno rozwiązanie gdy

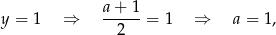
a-+-1- y = 1 ⇒ 2 = 1 ⇒ a = 1,

dwa rozwiązania gdy

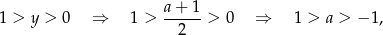
a + 1 1 > y > 0 ⇒ 1 > --2---> 0 ⇒ 1 > a > − 1,

i nie będzie miało rozwiązań w pozostałych przypadkach. Zatem liczba rozwiązań układu równań wynosi

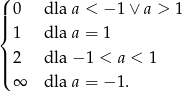
( 0 dla a < − 1∨ a > 1 |||{ 1 dla a = 1 | 2 dla − 1 < a < 1 ||( ∞ dla a = − 1.

Sposób II

Zadanie ma też dość prostą interpretację geometryczną.

PIC

Jeżeli zapiszemy pierwsze równanie w postaci

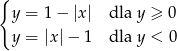
{ y = 1 − |x| dla y ≥ 0 y = |x|− 1 dla y < 0

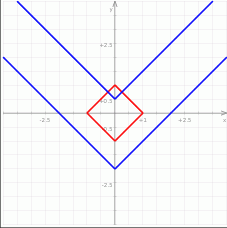
to łatwo naszkicować rozwiązania tego równania: jest kwadrat o wierzchołkach

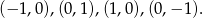
(− 1,0),(0,1),(1,0),(0,− 1).

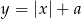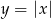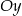Zatem pytamy się ile punktów wspólnych ma ten kwadrat z wykresem funkcji y = |x |+ a , który to wykres powstaje przez przesunięcie wykresu y = |x | o a wzdłuż osi Oy . Przy takiej interpretacji, otrzymana wcześniej odpowiedź staje się oczywista.

Wersja PDF