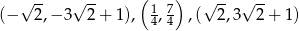/Szkoła średnia/Funkcje - wykresy/Wielomiany

Zadanie nr 4071151

Dodaj do ulubionych
Dodaj do rozwiązanych

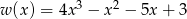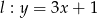Wyznacz punkty wspólne wykresu wielomianu 3 2 w (x) = 4x − x − 5x + 3 i prostej l : y = 3x + 1 .

Rozwiązanie

Musimy rozwiązać równanie 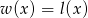w (x) = l(x ) .

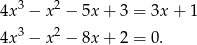
3 2 4x − x − 5x+ 3 = 3x + 1 4x 3 − x2 − 8x+ 2 = 0.

Jeżeli ktoś ma sprawne oczy to może rozłożyć lewą stronę bezpośrednio:

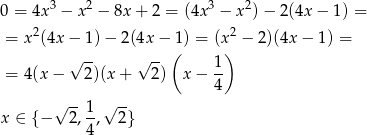
0 = 4x 3 − x 2 − 8x + 2 = (4x3 − x2) − 2(4x − 1 ) = 2 2 = x (4x − 1 )− 2 (4x− 1) = (x − 2)(4x − 1) = √ -- √ --( 1) = 4(x − 2)(x + 2) x− -- 4 √ -- 1-√ -- x ∈ {− 2, 4, 2}

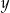Musimy do tych wartości x wyliczyć odpowiadające wartości y (najlepiej z równania prostej) i dostajemy punkty

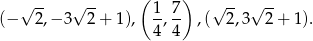
( ) √ -- √ -- 1-7- √ -- √ -- (− 2 ,− 3 2+ 1), 4,4 ,( 2,3 2+ 1).

Na koniec obrazek.

PIC

 
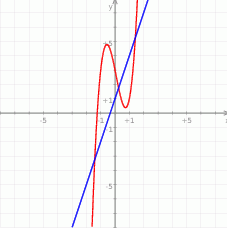
Odpowiedź: √ -- √ -- ( ) √ -- √ -- (− 2,− 3 2 + 1), 14, 74 ,( 2,3 2 + 1)

Wersja PDF