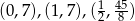/Szkoła średnia/Funkcje - wykresy/Wielomiany

Zadanie nr 6660055

Wyznacz punkty wspólne wykresów funkcji 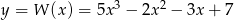3 2 y = W (x) = 5x − 2x − 3x + 7 oraz y = W (1− x) .

Wersja PDF

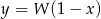Rozwiązanie

Musimy rozwiązać równanie

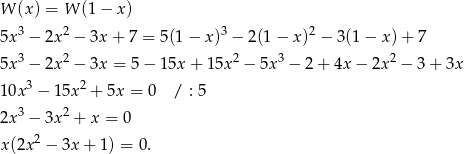
W (x) = W (1 − x) 5x 3 − 2x 2 − 3x+ 7 = 5(1 − x)3 − 2(1 − x )2 − 3(1 − x )+ 7 3 2 2 3 2 5x − 2x − 3x = 5 − 15x + 15x − 5x − 2 + 4x − 2x − 3 + 3x 10x 3 − 15x2 + 5x = 0 / : 5 2x 3 − 3x 2 + x = 0 2 x (2x − 3x + 1) = 0.

Zatem jeden punkt wspólny wykresów to

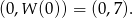
(0,W (0)) = (0 ,7 ).

Aby znaleźć pozostałe, musimy rozwiązać równanie kwadratowe w nawiasie.

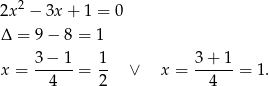
2x2 − 3x + 1 = 0 Δ = 9 − 8 = 1 3 − 1 1 3 + 1 x = ------= -- ∨ x = ------= 1. 4 2 4

Daje to nam punkty

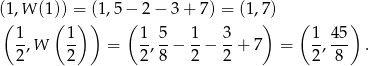
(1,W (1)) = (1,5 − 2 − 3 + 7) = (1 ,7) ( ( ) ) ( ) ( ) 1- 1- 1- 5- 1- 3- 1-45- 2,W 2 = 2, 8 − 2 − 2 + 7 = 2, 8 .

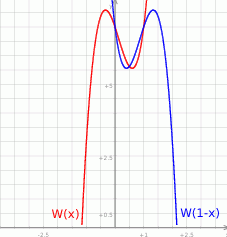
Na zakończenie, dla ciekawskich, wykresy funkcji 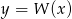y = W (x ) i y = W (1 − x) .

PIC

 
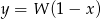Odpowiedź: (0,7 ),(1 ,7),(12, 458 )

Wersja PDF