Zadanie nr 6756430
Wielomian stopnia trzeciego 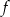 , którego fragment wykresu przedstawiono na poniższym rysunku spełnia warunek
, którego fragment wykresu przedstawiono na poniższym rysunku spełnia warunek 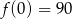 .
.
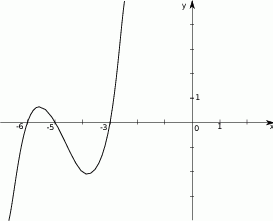
Wielomian 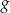 dany jest wzorem
dany jest wzorem 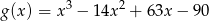 . Wykaż, że
. Wykaż, że 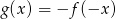 dla
dla 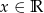 .
.
Rozwiązanie
Ponieważ wielomian jest stopnia 3 i liczby 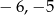 i
i 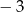 są jego pierwiastkami, to musi on być postaci
są jego pierwiastkami, to musi on być postaci
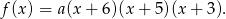
Ponieważ 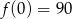 , to
, to 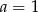 . Zatem
. Zatem