Zadanie nr 4731595
W kąt o mierze 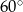 wpisano pięć kół tak, że każde następne koło poza pierwszym, jest styczne zewnętrznie do koła poprzedniego. Oblicz ile razy suma pól wszystkich kół jest większa od pola najmniejszego koła.
wpisano pięć kół tak, że każde następne koło poza pierwszym, jest styczne zewnętrznie do koła poprzedniego. Oblicz ile razy suma pól wszystkich kół jest większa od pola najmniejszego koła.
Rozwiązanie
Zaczynamy od rysunku – rysujemy dwa sąsiednie koła i spróbujemy ustalić jaki jest związek między ich promieniami.
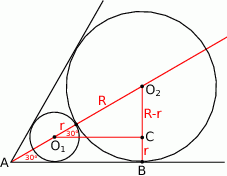
Przyjmijmy oznaczenia z rysunku, tzn. mniejszy okrąg niech ma środek 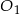 i promień
i promień  , a większy środek
, a większy środek 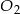 i promień
i promień 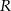 . Ponadto niech
. Ponadto niech 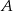 będzie wierzchołkiem kąta, a
będzie wierzchołkiem kąta, a 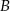 punktem styczności większego okręgu z ramieniem kąta.
punktem styczności większego okręgu z ramieniem kąta.
Zauważmy, że środki okręgów wpisanych w kąt leżą na dwusiecznej tego kąta, czyli
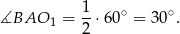
Niech 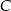 będzie punktem wspólnym promienia
będzie punktem wspólnym promienia 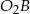 i prostej równoległej do ramienia
i prostej równoległej do ramienia 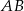 kąta, która przechodzi przez
kąta, która przechodzi przez 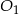 . Otrzymany trójkąt
. Otrzymany trójkąt 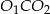 jest prostokątny i
jest prostokątny i
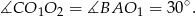
Ponadto 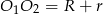 i
i 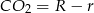 , czyli
, czyli
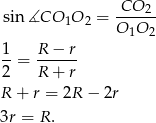
Wiemy już jaka jest zależność między promieniami kolejnych okręgów, więc wracamy do treści zadania. Jeżeli przez  oznaczmy promień najmniejszego okręgu wpisanego w kąt, to kolejne okręgi mają promienie
oznaczmy promień najmniejszego okręgu wpisanego w kąt, to kolejne okręgi mają promienie 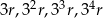 i interesujący nas stosunek pól jest równy
i interesujący nas stosunek pól jest równy
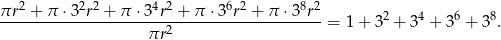
Otrzymaną sumę możemy obliczyć na kalkulatorze, ale możemy też skorzystać ze wzoru na sumę kolejnych wyrazów ciągu geometrycznego. Mamy ciąg, w którym 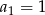 i
i 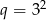 , czyli
, czyli
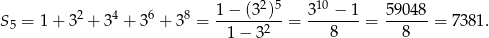
Odpowiedź: 7381 razy.

