/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Styczność/Wpisane w kąt

Zadanie nr 6002085

W kąt o mierze 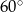∘ 60 wpisano dwa okręgi styczne zewnętrznie. Promień mniejszego okręgu ma długość 1. Oblicz długość promienia drugiego okręgu.

Wersja PDF

Rozwiązanie

Zacznijmy od rysunku.

PIC

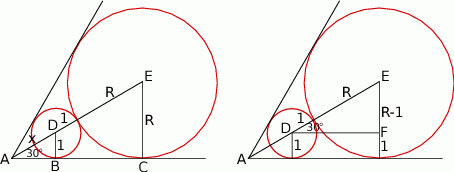
Sposób I

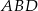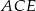Kluczowe w tym zadaniu jest podobieństwo trójkątów ABD i ACE . Zanim je jednak wykorzystamy, wyliczmy długość 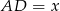AD = x . Patrzymy na trójkąt ABD .

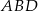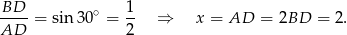
BD ∘ 1 ---- = sin 30 = -- ⇒ x = AD = 2BD = 2. AD 2

Teraz skorzystajmy z podobieństwa trójkątów 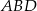ABD i ACE

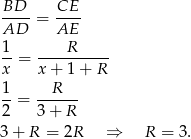
BD-- -CE- AD = AE 1 R --= ---------- x x + 1 + R 1- --R--- 2 = 3+ R 3+ R = 2R ⇒ R = 3.

Sposób II

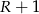Tym razem popatrzmy na trójkąt prostokątny DF E . Łatwo się przekonać, że jego przeciwprostokątna ma długość R + 1 , a przyprostokątna 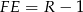FE = R − 1 . Ponieważ kąt ostry 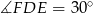∡F DE = 30∘ , mamy

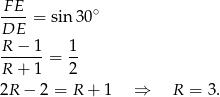
F-E- ∘ DE = sin30 R − 1 1 ------ = -- R + 1 2 2R − 2 = R + 1 ⇒ R = 3.

 
Odpowiedź: 3

Wersja PDF