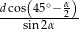/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny/Okręgi

Zadanie nr 6377690

Dodaj do ulubionych
Dodaj do rozwiązanych

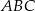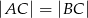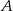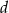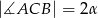W rozwartokątnym trójkącie równoramiennym ABC (|AC | = |BC | ) odległość środka koła wpisanego w trójkąt od wierzchołka A jest równa d , a |∡ACB | = 2α . Oblicz pole trójkąta 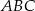ABC i promień koła opisanego na trójkącie ABC .

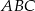Rozwiązanie

Oznaczmy 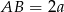AB = 2a i CD = h .

PIC

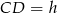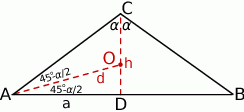
Jeżeli połączymy dwusieczną wierzchołek A ze środkiem okręgu wpisanego, to mamy

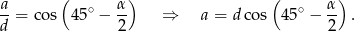
a ( α) ( α ) --= co s 4 5∘ − -- ⇒ a = dcos 45∘ − -- . d 2 2

Ponadto

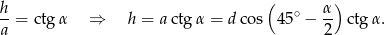
h ( α) --= ctg α ⇒ h = actgα = dc os 45∘ − -- ctg α. a 2

Zatem pole jest równe

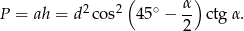
( ) 2 2 ∘ α- P = ah = d cos 45 − 2 ctg α.

Promień okręgu opisanego wyliczamy z twierdzenia sinusów.

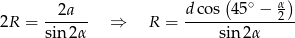
( α) --2a-- d-cos-4-5∘ −-2- 2R = sin2α ⇒ R = sin 2α

 
Odpowiedź: Pole: 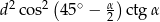d2cos2 (45∘ − α) ctgα 2 , promień: ∘ α dcoss(in452−α-2)

Wersja PDF