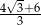/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny/Okręgi

Zadanie nr 8710321

W trójkącie równoramiennym kąt przy wierzchołku ma miarę 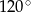∘ 12 0 . Wyznacz stosunek długości promienia okręgu opisanego na tym trójkącie do długości promienia okręgu wpisanego w ten trójkąt.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

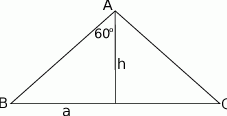
Jeżeli oznaczymy 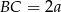BC = 2a to z twierdzenia sinusów łatwo wyliczyć promień okręgu opisanego

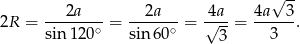
√ -- --2a---- --2a--- -4a- 4a---3 2R = sin 120∘ = sin6 0∘ = √ 3-= 3 .

Promień okręgu wpisanego wyliczymy ze wzoru 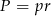P = pr , gdzie 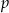p jest połową obwodu. Mamy

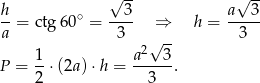
√ -- √ -- h-= ctg6 0∘ = --3- ⇒ h = a--3- a 3 √ -- 3 1 a 2 3 P = --⋅(2a) ⋅h = ------. 2 3

Pozostało wyliczyć połowę obwodu.

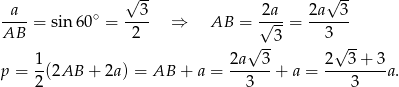
√ -- √ -- a 3 2a 2a 3 ----= sin 60∘ = ---- ⇒ AB = √---= ------ AB 2 √ --3 3√ -- 1 2a 3 2 3 + 3 p = --(2AB + 2a) = AB + a = ------+ a = ---------a. 2 3 3

Możemy teraz wyliczyć promień

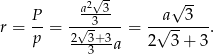
a2√3 √ -- r = P-= -√-3----= -√a--3--. p 2-3+-3a 2 3+ 3 3

Zatem stosunek promieni jest równy

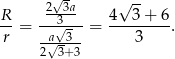
2√-3a √ -- R- = ---3√-- = 4--3-+-6. r √a-3-- 3 2 3+3

 
Odpowiedź: √ - 4--33+6

Wersja PDF