Zadanie nr 9873836
W trójkąt równoramienny o ramieniu 10 i podstawie 12 wpisano prostokąt o stosunku boków 1:4 w ten sposób, ze krótszy bok jest zawarty w podstawie trójkąta. Oblicz długości boków prostokąta.
Rozwiązanie
Zaczynamy od rysunku.
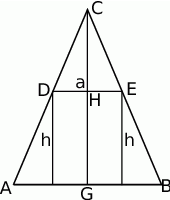
Oznaczmy poziomy bok (podstawę) prostokąta przez  , a jego wysokość przez
, a jego wysokość przez 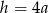 . Z twierdzenia Pitagorasa w trójkącie
. Z twierdzenia Pitagorasa w trójkącie 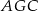 możemy wyliczyć długość wysokości
możemy wyliczyć długość wysokości 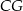 trójkąta
trójkąta 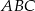 .
.
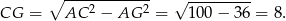
Korzystamy teraz z podobieństwa trójkątów 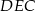 i
i 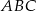 .
.
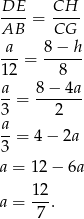
Zatem 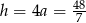
Odpowiedź: 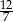 i
i