/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny/Oblicz długość...

Zadanie nr 4029066

Na trójkącie równoramiennym 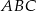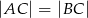ABC (|AC | = |BC | ) o polu równym 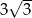√ -- 3 3 opisano okrąg, którego promień ma długość 2 cm. Oblicz długość wysokości 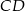CD tego trójkąta.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

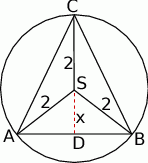
Jeżeli 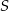S jest środkiem okręgu opisanego i oznaczymy 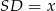SD = x , to z twierdzenia Pitagorasa w trójkącie 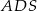ADS mamy

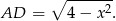
∘ ------- AD = 4 − x2.

Zatem warunek z polem daje nam równanie

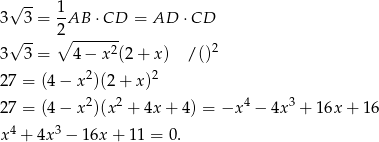
-- 3√ 3 = 1AB ⋅CD = AD ⋅CD 2 √ -- ∘ -----2- 2 3 3 = 4 − x (2 + x) /() 27 = (4− x 2)(2+ x)2 2 2 4 3 27 = (4− x )(x + 4x+ 4) = −x − 4x + 16x + 16 x4 + 4x3 − 16x + 11 = 0.

Szukamy pierwiastka całkowitego – jeden z nich to 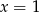x = 1 . Dzielimy przez 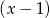(x − 1) , my zrobimy to grupując wyrazy.

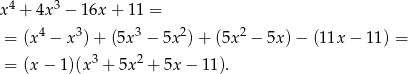
4 3 x + 4x − 16x + 11 = = (x4 − x3) + (5x 3 − 5x 2)+ (5x 2 − 5x)− (11x − 11) = = (x − 1)(x 3 + 5x 2 + 5x− 11).

Otrzymany wielomian stopnia 3 również ma pierwiastek 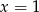x = 1 , więc znowu dzielimy przez (x − 1) .

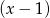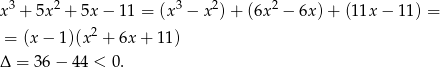
3 2 3 2 2 x + 5x + 5x − 11 = (x − x )+ (6x − 6x) + (11x − 11 ) = = (x − 1)(x2 + 6x + 1 1) Δ = 36− 44 < 0.

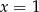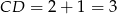Zatem x = 1 i wysokość ma długość CD = 2+ 1 = 3 .  
Odpowiedź: CD = 3

Wersja PDF