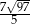Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 7282676

W trójkąt równoramienny 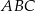ABC o podstawie długości 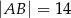|AB | = 14 i polu 168 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek 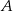A z punktem wspólnym okręgu i ramienia BC .

Wersja PDF
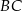Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

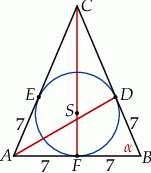
Z podanego pola obliczamy długość wysokości i ramienia trójkąta.

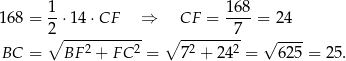
168 = 1-⋅14 ⋅CF ⇒ CF = 16-8 = 24 2∘ ----------- ∘ -------7- √ ---- BC = BF 2 + FC 2 = 72 + 242 = 6 25 = 25.

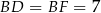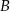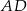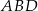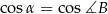Zauważmy teraz, że BD = BF = 7 , bo są to odcinki stycznych do okręgu wpisanego poprowadzonych z punktu B . Możemy więc obliczyć długość odcinka AD stosując twierdzenie cosinusów w trójkącie ABD . Najpierw obliczamy cosα = cos∡B .

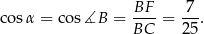
cos α = cos ∡B = BF--= -7. BC 25

Teraz piszemy twierdzenie cosinusów w trójkącie ABD .

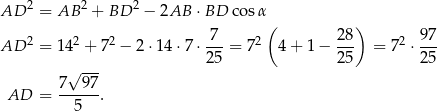
2 2 2 AD = AB + BD − 2AB ⋅BD cosα 7 ( 28 ) 97 AD 2 = 142 + 72 − 2⋅14 ⋅7 ⋅---= 72 4 + 1 − --- = 72 ⋅--- √ --- 25 25 25 7 97 AD = ------. 5

 
Odpowiedź: √ -- 7-597

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!