/Szkoła średnia/Ciągi/Dowolny

Zadanie nr 2266099

Dodaj do ulubionych
Dodaj do rozwiązanych

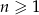Suma n ≥ 1 początkowych wyrazów ciągu 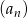(an ) wyraża się wzorem 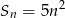Sn = 5n2 . Oblicz, ile wyrazów tego ciągu jest liczbami trzycyfrowymi.

Rozwiązanie

Zauważmy, że mając wzór na sumę początkowych wyrazów ciągu, możemy obliczyć jego wyrazy. Dokładniej, 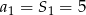a1 = S1 = 5 , a jeżeli 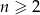n ≥ 2 to

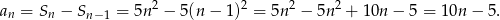
an = Sn − Sn −1 = 5n 2 − 5 (n− 1)2 = 5n2 − 5n 2 + 10n − 5 = 10n − 5 .

Pozostało teraz rozwiązać nierówność

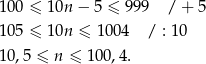
100 ≤ 10n − 5 ≤ 999 / + 5 105 ≤ 10n ≤ 100 4 / : 10 10,5 ≤ n ≤ 100,4.

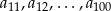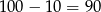W takim razie liczbami trzycyfrowymi są wyrazy: a11,a12,...,a100 . Jest ich 10 0− 1 0 = 90 .  
Odpowiedź: 90 wyrazów.

Wersja PDF