Zadanie nr 2569923

Dany jest ciąg określony wzorem 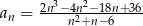2n3−4n2−18n+36 an = n2+n−6 .

Rozwiązanie

Sposób I

Rozłóżmy wielomian w liczniku ułamka deﬁniującego ciąg 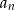. Łatwo to zrobić grupując wyrazy.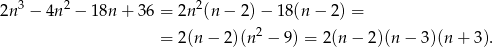

$3 2 2 2n − 4n − 18n + 36 = 2n (n− 2)− 18(n − 2) = = 2(n − 2 )(n2 − 9) = 2(n − 2)(n − 3 )(n + 3).$

Teraz rozkładamy trójmian w mianowniku.

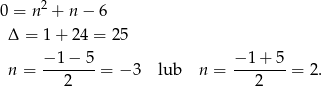
$2 0 = n + n − 6 Δ = 1 + 2 4 = 25 n = −-1-−-5 = − 3 lub n = −-1-+-5 = 2. 2 2$

Mamy zatem

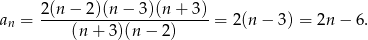
$2(n − 2)(n − 3 )(n+ 3) an = ----------------------- = 2(n − 3 ) = 2n − 6. (n + 3)(n − 2 )$

Widać teraz, że wszystkie wyrazy ciągu 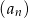są faktycznie liczbami całkowitymi.

Sposób II

Aby wykazać, że każdy wyraz ciągu jest liczbą całkowitą, spróbujmy podzielić 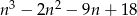przez 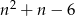. My zrobimy to grupując wyrazy.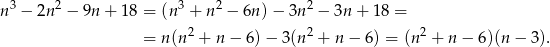

$3 2 3 2 2 n − 2n − 9n + 18 = (n + n − 6n)− 3n − 3n + 18 = = n (n2 + n − 6) − 3(n2 + n − 6) = (n 2 + n− 6)(n − 3).$

Mamy zatem

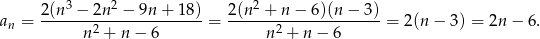
$3 2 2 a = 2(n--−-2n--−--9n-+-18) = 2(n--+-n-−-6)(n-−-3-)= 2(n − 3) = 2n − 6. n n2 + n − 6 n2 + n − 6$

Widać teraz, że wszystkie wyrazy ciągu 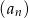są faktycznie liczbami całkowitymi.
Zauważmy, że podany ciąg
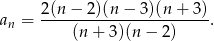
$a = 2(n−--2)(n-−-3)(n-+-3)-. n (n+ 3)(n − 2)$

nie jest określony dla 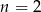(choć jest określony dla 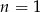i 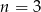), więc nie jest ciągiem arytmetycznym.
Odpowiedź: Nie, nie jest arytmetyczny.