/Szkoła średnia/Ciągi/Dowolny

Zadanie nr 5387765

Dodaj do ulubionych
Dodaj do rozwiązanych

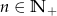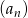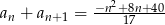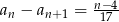Dla każdego n ∈ N + wyrazy ciągu (an) spełniają dwa warunki 2 an + an+ 1 = −n-+187n+40 i an − an+1 = n−174- . Oblicz, które wyrazy tego ciągu są dodatnie.

Rozwiązanie

Dodając dwie dane równości stronami (żeby zredukować 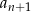an+ 1 ) otrzymujemy

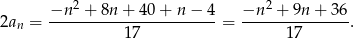
2 2 2an = −n--+--8n+--40-+-n-−-4-= −n--+--9n-+-36-. 17 17

Ponieważ mianownik jest zawsze dodatni, wystarczy sprawdzić, kiedy dodatni jest licznik.

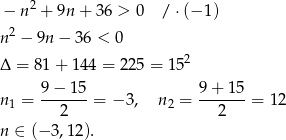
2 − n + 9n + 36 > 0 / ⋅(− 1) n 2 − 9n − 36 < 0 Δ = 81 + 14 4 = 225 = 1 52 9 − 15 9+ 15 n 1 = -------= − 3, n2 = -------= 12 2 2 n ∈ (−3 ,12).

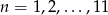Ponieważ interesują nas tylko dodatnie wartości n , mamy n = 1,2,...,11 .  
Odpowiedź: a1,a2,...,a11

Wersja PDF