/Szkoła średnia/Ciągi/Dowolny

Zadanie nr 7132111

Dodaj do ulubionych
Dodaj do rozwiązanych

Nieskończony ciąg liczbowy 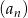(an) określony jest wzorem:

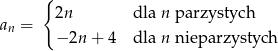
{ a = 2n dla n parzystych n − 2n + 4 dla n nieparzystych
  • Wyznacz sumę dwudziestu początkowych wyrazów ciągu.
  • Zbadaj, czy istnieje wyraz ciągu równy 5. Odpowiedź uzasadnij.

Rozwiązanie

  •  

    Sposób I

    Liczymy

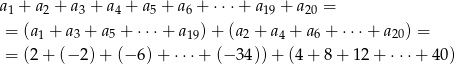
    a 1 + a2 + a3 + a4 + a5 + a6 + ⋅⋅⋅+ a19 + a20 = = (a1 + a 3 + a5 + ⋅⋅⋅ + a19)+ (a2 + a4 + a6 + ⋅⋅⋅+ a20) = = (2+ (− 2 )+ (− 6) + ⋅⋅⋅+ (− 34))+ (4+ 8+ 12+ ⋅⋅⋅+ 4 0)

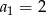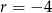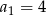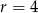    Teraz wystarczy zauważyć, że w pierwszym nawiasie mamy sumę 10 początkowych wyrazów ciągu arytmetycznego, w którym a = 2 1 i r = − 4 , a w drugim nawiasie sumę dziesięciu początkowych wyrazów ciągu arytmetycznego, w którym a1 = 4 i r = 4 . Ze wzoru na sumę wyrazów ciągu arytmetycznego mamy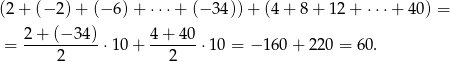

    (2+ (− 2)+ (− 6) + ⋅⋅⋅ + (− 34)) + (4+ 8+ 12 + ⋅⋅⋅+ 40) = = 2-+-(−-34)-⋅10 + 4-+-40-⋅1 0 = − 160 + 220 = 60. 2 2

    Sposób II

    Zauważmy, że suma dwóch kolejnych wyrazów danego ciągu jest równa 6. Rzeczywiście:

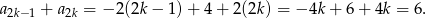
    a2k− 1 + a2k = − 2(2k − 1 )+ 4 + 2(2k ) = − 4k+ 6+ 4k = 6.

    Zatem

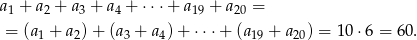
    a1 + a2 + a3 + a4 + ⋅ ⋅⋅+ a19 + a20 = = (a1 + a2) + (a3 + a4)+ ⋅⋅⋅+ (a19 + a20) = 10 ⋅6 = 60 .

     
    Odpowiedź: 60

  •  

    Sposób I

    Ze wzoru ciągu widać, że każdy wyraz jest liczbą parzystą, zatem żaden z wyrazów nie może być równy 5.

    Sposób II

    Zauważmy, że

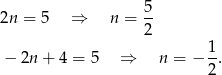
    2n = 5 ⇒ n = 5- 2 1- − 2n + 4 = 5 ⇒ n = − 2.

    Zatem żaden z wyrazów ciągu nie może być równy 5.  
    Odpowiedź: Nie, nie istnieje.

Wersja PDF