/Szkoła średnia/Ciągi/Dowolny

Zadanie nr 7168025

Dodaj do ulubionych
Dodaj do rozwiązanych

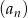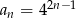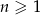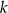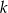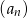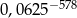Ciąg (an) jest określony wzorem 2n− 1 an = 4 , gdzie n ≥ 1 . Wyznacz wszystkie wartości k , dla których iloczyn k początkowych wyrazów ciągu (an) jest równy 0,06 25−578 .

Rozwiązanie

Musimy rozwiązać równanie

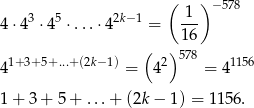
( )− 578 4 ⋅43 ⋅45 ⋅ ...⋅42k−1 = -1- 16 ( )578 4 1+ 3+5+...+(2k−1) = 4 2 = 41156 1 + 3 + 5 + ...+ (2k− 1) = 1156 .

Widać teraz, że lewa strona jest sumą 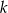k początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie równym 1 i 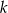k -tym równym 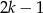2k − 1 . Mamy zatem

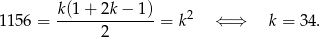
k(1-+-2k-−-1)- 2 1156 = 2 = k ⇐ ⇒ k = 34.

 
Odpowiedź: k = 3 4

Wersja PDF