/Szkoła średnia/Ciągi/Dowolny

Zadanie nr 8118818

Dodaj do ulubionych
Dodaj do rozwiązanych

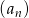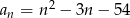Ciąg (an) określony jest wzorem 2 an = n − 3n − 54 .

  • Nie korzystając z kalkulatora, rozstrzygnij, czy 58 wyraz ciągu 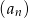(an) jest kwadratem liczby naturalnej.
  • Znajdź takie dwa kolejne wyrazy ciągu 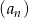(a ) n , aby ich rożnica była równa 20.

Rozwiązanie

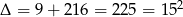  • Wzór ciągu jest funkcją kwadratową (zmiennej n ), sprawdźmy czy ma ona pierwiastki (żeby zapisać ten wzór w postaci iloczynowej). Δ = 9+ 216 = 225 = 152 . Stąd pierwiastki to -6 i 9 i mamy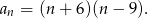
    an = (n+ 6)(n − 9).

    Liczymy teraz a58 :

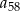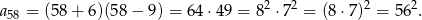
    2 2 2 2 a58 = (58+ 6)(58 − 9) = 64 ⋅49 = 8 ⋅7 = (8⋅7 ) = 56 .

     
    Odpowiedź: Tak

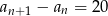  • Szukamy rozwiązań równania (z niewiadomoą n ): an+1 − an = 20 .
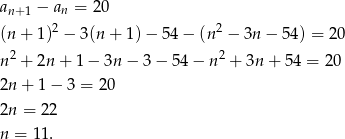
    an+1 − an = 20 (n + 1)2 − 3(n + 1) − 54 − (n2 − 3n − 5 4) = 20 2 2 n + 2n + 1 − 3n − 3 − 5 4− n + 3n+ 54 = 20 2n + 1 − 3 = 2 0 2n = 22 n = 1 1.

     
    Odpowiedź: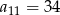 a 11 = 34 , a12 = 54

Wersja PDF