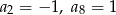Zadanie nr 8426126
Wyraz ogólny ciągu  dany jest wzorem
dany jest wzorem 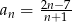 , gdzie
, gdzie 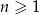 .
.
- Który wyraz ciągu
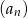 równa się
równa się 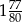 ?
? - Ile wyrazów danego ciągu należy do przedziału
 ?
? - Które wyrazy tego ciągu przyjmują wartości całkowite?
Rozwiązanie
- Liczymy
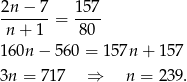
Odpowiedź: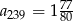
- Liczymy
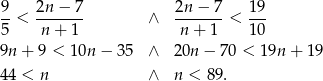
Wyrazów tych jest tyle ile liczby:
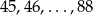 , czyli
, czyli 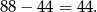
Odpowiedź: 44 wyrazy. - Przekształćmy wzór ciągu
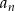 tak, aby usunąć z licznika
tak, aby usunąć z licznika  .
. 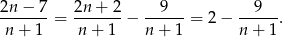
Teraz widać, że liczba ta będzie całkowita tylko jeżeli
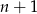 dzieli 9, czyli dla
dzieli 9, czyli dla 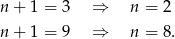
Odpowiedź: