Zadanie nr 8587713
Dany jest ciąg 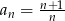 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 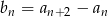 , gdzie
, gdzie 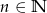 .
.
Rozwiązanie
Sposób I
Liczymy
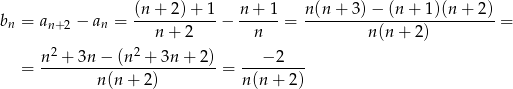
Sposób II
Tym razem będziemy odrobinę sprytniejsi i zauważmy, że 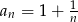 . Mamy zatem
. Mamy zatem
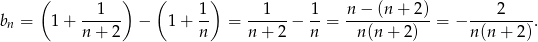
Odpowiedź: 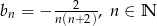
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest ciąg 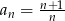 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 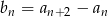 , gdzie
, gdzie 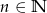 .
.
Sposób I
Liczymy
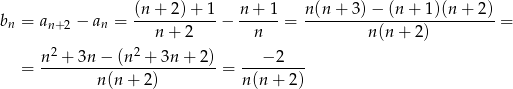
Sposób II
Tym razem będziemy odrobinę sprytniejsi i zauważmy, że 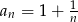 . Mamy zatem
. Mamy zatem
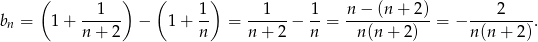
Odpowiedź: