/Szkoła średnia/Ciągi/Dowolny

Zadanie nr 9446709

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest ciąg o wyrazie ogólnym 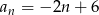an = − 2n + 6 . Wybierz sto kolejnych początkowych wyrazów ciągu 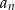an i oblicz dla jakiej liczby naturalnej 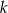k stosunek wyrazu stojącego na miejscu 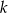k , licząc od początku, do wyrazu stojącego na miejscu 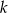k , licząc od końca, jest równy -3 16 .

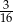Rozwiązanie

Wyraz stojący na miejscu 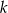k od początku, to

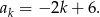
ak = − 2k + 6.

Wyraz stojący na miejscu 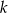k od końca, to

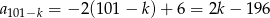
a 101−k = − 2(101 − k)+ 6 = 2k − 196

(jak ktoś nie wie czemu to niech podstawi sobie np. 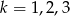k = 1,2,3 ). Ich iloraz to

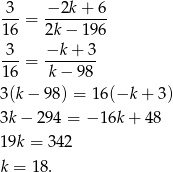
-3- = −-2k-+-6- 1 6 2k − 19 6 3 −k + 3 --- = ------- 1 6 k− 98 3(k − 98) = 16(−k + 3) 3k − 294 = − 16k + 48 19k = 342 k = 1 8.

 
Odpowiedź: k = 1 8

Wersja PDF