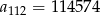/Szkoła średnia/Ciągi/Dowolny

Zadanie nr 9803000

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz największy wyraz ciągu 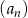(an) danego wzorem 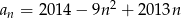2 an = 2014 − 9n + 2 013n , dla n ≥ 1 .

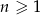Rozwiązanie

Wykresem funkcji kwadratowej 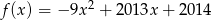2 f(x) = − 9x + 2013x + 20 14 jest parabola o ramionach skierowanych w dół i wierzchołku w punkcie

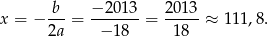
x = − -b-= −-2013-= 20-13 ≈ 111 ,8. 2a − 18 1 8

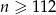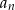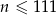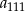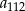To oznacza, że dla n ≥ 112 ciąg an jest malejący, a dla n ≤ 111 ciąg jest rosnący. Zatem największym wyrazem ciągu jest a111 lub a112 – który z nich? liczymy i sprawdzamy.

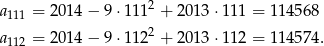
a111 = 2014 − 9 ⋅1112 + 2013 ⋅111 = 114568 2 a112 = 2014 − 9 ⋅112 + 2013 ⋅112 = 114574 .

Zatem 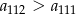a112 > a111 .  
Odpowiedź: a112 = 114 574

Wersja PDF