Zadanie nr 4904151

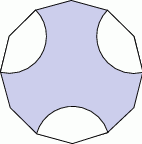
Z dwunastokąta foremnego odcięto trzy wycinki kół, których środkami są pewne wierzchołki dwunastokąta, a ich promienie mają długość równą długości boku dwunastokąta. Wiedząc, że suma pól tych wycinków jest równa 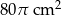80 π cm 2 , oblicz:

długość boku dwunastokąta;
długość promienia okręgu opisanego na tym dwunastokącie;
pole ﬁgury powstałej po odcięciu od dwunastokąta trzech danych wycinków kołowych.

Wersja PDF

Rozwiązanie

Połączmy środek dwunastokąta z wierzchołkami.

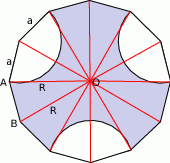
Otrzymamy wtedy 12 trójkątów równoramiennych, których kąt przy wierzchołku ma miarę

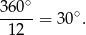
$360∘- ∘ 12 = 30 .$

Zatem kąt przy podstawie jest równy

$∘ ∘ 180--−-30--= 75∘. 2$

W takim razie każdy z zaznaczonych wycinków kołowych jest oparty o kąt środkowy 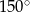, czyli ma pole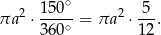

$∘ πa2 ⋅ 150-= πa 2 ⋅ 5-. 360 ∘ 12$

Daje to nam równanie

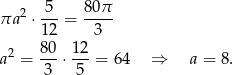
$2 5 80π πa ⋅12-= -3-- a2 = 80-⋅ 1-2 = 64 ⇒ a = 8. 3 5$

Odpowiedź: 8 cm
Piszemy twierdzenie cosinusów w trójkącie .
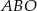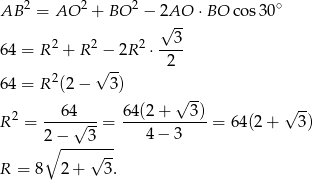
$2 2 2 ∘ AB = AO + BO − 2√AO- ⋅BO cos 30 2 2 2 3 64 = R + R − 2R ⋅ ---- 2 √ -- 2 64 = R (2 − 3) √ -- √ -- R 2 = ---64√---= 64(2-+---3)-= 64(2+ 3) 2 − 3 4 − 3 ∘ ----√--- R = 8 2 + 3 .$

Odpowiedź: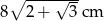
Policzmy pole dwunastokąta. Pole trójkąta 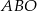jest równe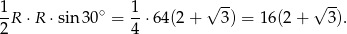
$√ -- √ -- 1R ⋅ R ⋅sin 30∘ = 1-⋅64(2 + 3) = 1 6(2+ 3). 2 4$

Zatem pole całego dwunastokąta jest równe

$√ -- √ -- 12 ⋅16(2 + 3) = 19 2(2+ 3).$

Od tego musimy odjąć pola wycinków kołowych.
Odpowiedź: