/Szkoła średnia/Geometria/Planimetria/Wielokąty/Różne

Zadanie nr 5826377

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz miarę kąta:

  • pięciokąta foremnego;
  • sześciokąta foremnego;
  • dziewięciokąta foremnego.

Rozwiązanie

Sposób I

Z jednego wierzchołka wielokąta foremengo wychodzi 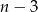n − 3 przekątnych.

PIC

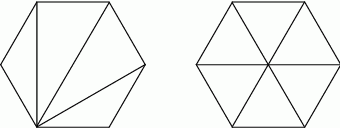
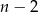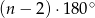Prowadząc je podzielimy wielokąt na n − 2 trójkątów, zatem suma wszystkich kątów w n -kącie wynosi ∘ (n − 2)⋅18 0 (ten sam argument pokazuje, że taka sama jest suma kątów dowolnego wielokąta wypukłego). Pojedyńczy kąt ma więc miarę 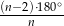∘ (n−-2)⋅180- n . W szczególności dla pięciokąta, sześciokąta i dziewięciokąta mamy odpowiednio 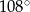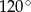108∘ , 120∘ i 140∘ .

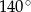Sposób II

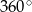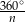Tym razem połączmy wierzchołki wielokąta foremnego z jego środkiem. Wokół środka mamy kąt ∘ 360 podzielony na n częsci, czyli na kąty 360∘ n . Zatem kąty przy podstawie utworzonych trójkątów równoramiennych są równe

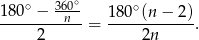
∘ 360∘ ∘ 1-80-−---n--= 180--(n−--2). 2 2n

Kąt wielokąta jest dwa razy większy, co daje nam ten sam wzór co poprzednio.  
Odpowiedź: 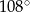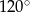10 8∘ , 120 ∘ i 140∘

Wersja PDF