Zadanie nr 6793781
Liczbę przekątnych wielokąta o  bokach można obliczyć ze wzoru
bokach można obliczyć ze wzoru 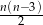 , gdzie
, gdzie 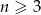 ,
, 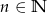 . Ile boków ma wielokąt, który ma 35 przekątnych?
. Ile boków ma wielokąt, który ma 35 przekątnych?
Rozwiązanie
Oznaczmy przez  szukaną liczbę boków. Wówczas otrzymujemy równanie
szukaną liczbę boków. Wówczas otrzymujemy równanie
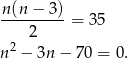
Obliczamy wyróżnik trójmianu
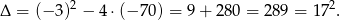
Wyznaczamy pierwiastki
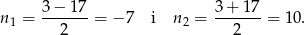
Liczba boków jest liczbą większą od zera, więc odrzucamy ujemny pierwiastek. Zatem liczba boków równa się 10.
Odpowiedź: 10

