Zadanie nr 1143096
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 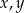 prawdziwa jest nierówność
prawdziwa jest nierówność
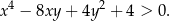
Rozwiązanie
Sposób I
Przekształcamy daną nierówność w sposób równoważny.
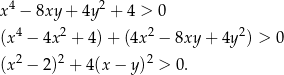
Otrzymana nierówność jest oczywiście spełniona (bo z założenia 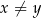 ), a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musiała być spełniona.
), a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musiała być spełniona.
Sposób II
Traktujemy lewą stronę nierówności jak funkcję kwadratową
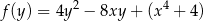
zmiennej 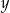 z parametrem
z parametrem  . Ponieważ
. Ponieważ
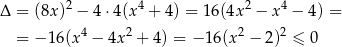
parabola będąca wykresem funkcji 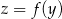 nigdy nie ma punktów leżących poniżej (poziomej!) osi
nigdy nie ma punktów leżących poniżej (poziomej!) osi 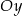 (dla
(dla 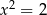 jest styczna do osi
jest styczna do osi 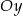 , a w pozostałych przypadkach leży w całości powyżej osi
, a w pozostałych przypadkach leży w całości powyżej osi 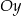 ). To oznacza, że faktycznie zawsze
). To oznacza, że faktycznie zawsze 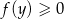 . Aby udowodnić ostrą nierówność zauważmy, że równość może zachodzić tylko gdy
. Aby udowodnić ostrą nierówność zauważmy, że równość może zachodzić tylko gdy 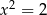 . Wtedy
. Wtedy
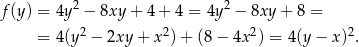
i równość 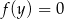 prowadzi do sprzeczności z założeniem
prowadzi do sprzeczności z założeniem 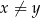 .
.

