Zadanie nr 2914848
Funkcja 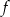 określona jest wzorem
określona jest wzorem 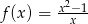 .
.
- Wykaż ze zbiorem wartości funkcji
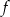 jest zbiór liczb rzeczywistych.
jest zbiór liczb rzeczywistych. - Uzasadnij, że funkcja
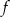 nie jest rożnowartościowa.
nie jest rożnowartościowa.
Rozwiązanie
- Musimy uzasadnić, że równanie
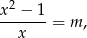
(z niewiadomą
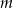 ) ma zawsze rozwiązanie. Liczymy (wyliczamy
) ma zawsze rozwiązanie. Liczymy (wyliczamy  )
) 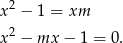
Dalej,
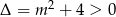 , co oznacza, że równanie to ma zawsze dwa różne rozwiązania. W szczególności jedno z nich jest niezerowe (musimy takie znaleźć, bo 0 nie należy do dziedziny funkcji
, co oznacza, że równanie to ma zawsze dwa różne rozwiązania. W szczególności jedno z nich jest niezerowe (musimy takie znaleźć, bo 0 nie należy do dziedziny funkcji 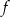 ).
). - Musimy znaleźć dwie wartości
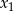 i
i 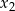 , dla których
, dla których 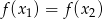 . Można spróbować zgadnąć, ale można też skorzystać z poprzedniego podpunktu. Uzasadniliśmy w nim, że każdą wartość funkcja
. Można spróbować zgadnąć, ale można też skorzystać z poprzedniego podpunktu. Uzasadniliśmy w nim, że każdą wartość funkcja 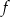 przyjmuje w 2 punktach (w zasadzie mogłoby się zdarzyć, że jednym z pierwiastków otrzymanego równania kwadratowego jest 0 i wtedy mamy tylko jednego
przyjmuje w 2 punktach (w zasadzie mogłoby się zdarzyć, że jednym z pierwiastków otrzymanego równania kwadratowego jest 0 i wtedy mamy tylko jednego  -a, a nie dwa, ale łatwo sprawdzić, że
-a, a nie dwa, ale łatwo sprawdzić, że 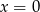 nigdy nie jest pierwiastkiem).
nigdy nie jest pierwiastkiem). Jeżeli chcemy mieć konkretny przykład, to biorąc np.
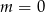 mamy
mamy 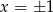 , czyli
, czyli