Zadanie nr 4252635
Ciąg 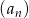 określony jest wzorem
określony jest wzorem 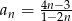 , dla
, dla 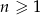 . Oblicz ile wyrazów ciągu
. Oblicz ile wyrazów ciągu 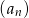 różni się od liczby -2 o więcej niż 0,1.
różni się od liczby -2 o więcej niż 0,1.
Rozwiązanie
Musimy rozwiązać nierówność
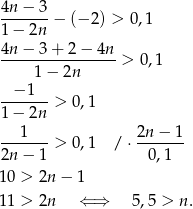
Odpowiedź: 5 pierwszych wyrazów.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Ciąg 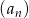 określony jest wzorem
określony jest wzorem 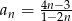 , dla
, dla 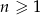 . Oblicz ile wyrazów ciągu
. Oblicz ile wyrazów ciągu 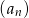 różni się od liczby -2 o więcej niż 0,1.
różni się od liczby -2 o więcej niż 0,1.
Musimy rozwiązać nierówność
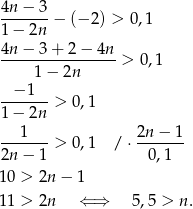
Odpowiedź: 5 pierwszych wyrazów.
