/Szkoła średnia/Ciągi/Dowolny/Wymierny

Zadanie nr 5133954

Ciąg 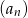(an) określony jest przez warunki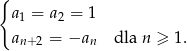 { a1 = a2 = 1 an+ 2 = −an dla n ≥ 1.

  • Wypisz 6 początkowych wyrazów ciągu (an) .
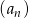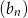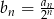  • Oblicz sumę 20 początkowych wyrazów ciągu (bn) danego wzorem b = an n 2n .
Wersja PDF

Rozwiązanie

  • Wypisujemy
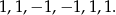
    1,1,− 1,− 1,1,1.

    Widać, że będą to na zmianę pary 1,1 i -1,-1.  
    Odpowiedź: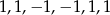 1,1,− 1,− 1,1,1

  • Wypiszmy kilka początkowych wyrazów ciągu bn .
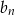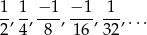
    1 1 − 1 − 1 1 -,--,---,---, --,... 2 4 8 16 32

    Widać, że jest to prawie ciąg geometryczny, problemem są tylko znaki. Jeżeli jednak osobno wypiszemy wyrazy parzyste i nieparzyste, to będziemy mieli prawdziwe ciągi geometryczne (o ilorazie −-1 4 ).

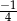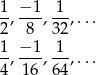
    1 − 1 1 -,----,--,... 2 8 32 1-−-1- -1- 4, 16 ,64,...

    Mamy obliczyć sumę 20 początkowych wyrazów ciągu 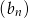(b ) n , więc musimy obliczyć sumę 10 wyrazów każdego z powyższych ciągów. Korzystamy ze wzoru na sumę początkowych wyrazów ciągu geometrycznego.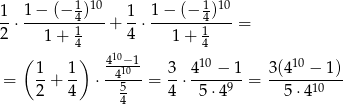

    1 10 1 10 1-⋅ 1-−-(−-4-) + 1⋅ 1−--(−-4)-- = 2 1 + 14 4 1+ 14 ( ) 410−1 1- 1- --410-- 3- 4-10-−-1 3(410 −-1) = 2 + 4 ⋅ 5 = 4 ⋅ 5 ⋅49 = 5 ⋅410 4

     
    Odpowiedź: 3(410−101) 5⋅4

Wersja PDF