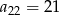/Szkoła średnia/Ciągi/Dowolny/Wymierny

Zadanie nr 6569995

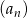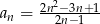Dany jest ciąg (an) o wyrazie ogólnym 2n2−-3n+-1 an = 2n− 1 .

  • Uzasadnij, że wszystkie wyrazy ciągu 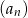(an) są liczbami całkowitymi.
  • Który wyraz jest równy 5?
  • Różnica sześcianów dwóch kolejnych wyrazów ciągu 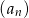(an) wynosi 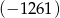(− 1261) . Wyznacz te wyrazy.
Wersja PDF

Rozwiązanie

  •  

    Sposób I

    Rozłóżmy trójmian w liczniku ułamka definiującego ciąg an .

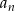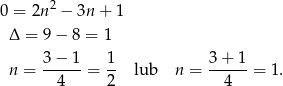
    0 = 2n 2 − 3n + 1 Δ = 9 − 8 = 1 n = 3-−-1-= 1- lub n = 3+--1-= 1. 4 2 4

    Stąd

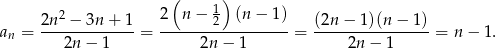
    ( 1) 2n 2 − 3n + 1 2 n − 2 (n− 1) (2n− 1)(n − 1) an = ------------- = ------------------= ----------------= n− 1. 2n − 1 2n − 1 2n − 1

    Widać teraz, że wszystkie wyrazy ciągu 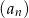(an ) są faktycznie liczbami całkowitymi.

    Sposób II

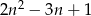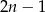    Aby wykazać, że każdy wyraz ciągu jest liczbą całkowitą, spróbujmy podzielić 2 2n − 3n + 1 przez 2n − 1 . My zrobimy to grupując wyrazy.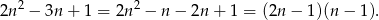

    2n2 − 3n + 1 = 2n 2 − n− 2n + 1 = (2n − 1)(n− 1).

    Mamy zatem

    an = n − 1 .

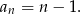
    Widać teraz, że wszystkie wyrazy ciągu 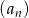(an ) są faktycznie liczbami całkowitymi.

  • Z poprzedniego punktu jest jasne, że a6 = 5 .  
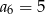    Odpowiedź: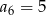 a = 5 6
  • Musimy rozwiązać równanie (z niewiadomą n )
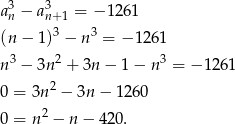
    3 3 an − an+ 1 = − 1261 (n − 1 )3 − n 3 = − 1261 n 3 − 3n 2 + 3n − 1− n3 = − 126 1 2 0 = 3n − 3n − 126 0 0 = n2 − n − 420.

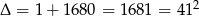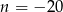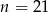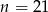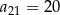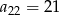    Rozwiązujemy to równanie kwadratowe 2 Δ = 1+ 1680 = 1 681 = 41 , n = − 20 lub n = 21 . Ujemne rozwiązanie odrzucamy i zostaje n = 21 . Zatem szukane wyrazy to a21 = 20 i a22 = 21 .  
    Odpowiedź: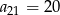 a21 = 20 i a22 = 21

Wersja PDF