/Szkoła średnia/Ciągi/Dowolny/Wymierny

Zadanie nr 7875576

Wyznacz wszystkie wyrazy nieskończonego ciągu 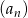(an ) określonego wzorem 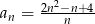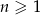2 an = 2n−nn-+4- , n ≥ 1 , które są liczbami całkowitymi.

Wersja PDF

Rozwiązanie

Przekształcamy wzór na wyrazy ciągu

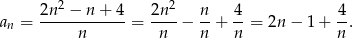
2 2 an = 2n--−--n+--4 = 2n--− n-+ 4-= 2n− 1+ 4-. n n n n n

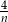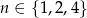Liczb ta jest liczbą całkowitą wtedy i tylko wtedy, gdy 4 n jest liczbą całkowitą, czyli wtedy, gdy n jest dzielnikiem 4. Tak będzie tylko dla n ∈ {1 ,2 ,4} . Mamy wtedy

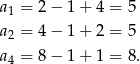
a1 = 2− 1+ 4 = 5 a = 4− 1+ 2 = 5 2 a4 = 8− 1+ 1 = 8.

 
Odpowiedź: a1 = a2 = 5, a 4 = 8

Wersja PDF