Zadanie nr 1566108
Ciąg 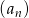 jest określony wzorem
jest określony wzorem 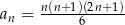 dla
dla 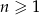 . Wykaż, że każdy kolejny wyraz tego ciągu jest większy od poprzedniego wyrazu o kwadrat liczby naturalnej.
. Wykaż, że każdy kolejny wyraz tego ciągu jest większy od poprzedniego wyrazu o kwadrat liczby naturalnej.
Rozwiązanie
Obliczamy różnicę dwóch kolejnych wyrazów ciągu 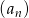 :
:
![(n+ 1)(n + 2)(2(n + 1) + 1) n(n + 1)(2n + 1 ) an+1 − an = -----------------------------− -----------------= 6 6 = n+--1-⋅(n + 2 )(2n + 3)− n(2n + 1 ) = 6 [ ] n+ 1 [ 2 2 ] = ------⋅ 2n + 3n + 4n + 6− 2n − n = 6 = n+--1-⋅(6n + 6) = (n + 1)2. 6](https://img.zadania.info/zad/1566108/HzadR1x.gif)
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Ciąg 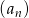 jest określony wzorem
jest określony wzorem 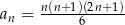 dla
dla 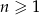 . Wykaż, że każdy kolejny wyraz tego ciągu jest większy od poprzedniego wyrazu o kwadrat liczby naturalnej.
. Wykaż, że każdy kolejny wyraz tego ciągu jest większy od poprzedniego wyrazu o kwadrat liczby naturalnej.
Obliczamy różnicę dwóch kolejnych wyrazów ciągu 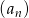 :
:
![(n+ 1)(n + 2)(2(n + 1) + 1) n(n + 1)(2n + 1 ) an+1 − an = -----------------------------− -----------------= 6 6 = n+--1-⋅(n + 2 )(2n + 3)− n(2n + 1 ) = 6 [ ] n+ 1 [ 2 2 ] = ------⋅ 2n + 3n + 4n + 6− 2n − n = 6 = n+--1-⋅(6n + 6) = (n + 1)2. 6](https://img.zadania.info/zad/1566108/HzadR1x.gif)
