/Szkoła średnia/Ciągi/Dowolny/Różne

Zadanie nr 2293817

Wykazać, że 1 nie jest wyrazem ciągu 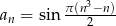π(n3−n) an = sin 2 .

Wersja PDF

Rozwiązanie

Próbujemy znaleźć liczbę naturalną 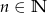n ∈ N spełniającą równanie

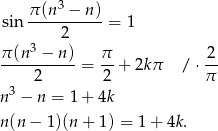
3 sin π-(n-−--n)-= 1 2 π-(n3-−-n)- π- 2- 2 = 2 + 2kπ / ⋅π 3 n − n = 1+ 4k n(n − 1 )(n+ 1) = 1 + 4k.

Zauważmy teraz, że powyższe równanie nie może mieć rozwiązań całkowitych, bo lewa strona równania jest zawsze liczbą parzystą (jako iloczyn trzech kolejnych liczb całkowitych), a prawa liczbą nieparzystą.

Wersja PDF