Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 5252388

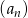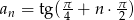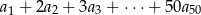Ciąg (an) dany jest wzorem π- π- an = tg (4 + n ⋅ 2) . Oblicz sumę a1 + 2a2 + 3a3 + ⋅⋅⋅+ 50a50 .

Wersja PDF
Rozwiązanie

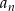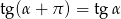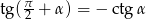Spróbujmy rozszyfrować czym jest ciąg an . Policzmy kilka jego pierwszych wyrazów (korzystamy z tego, że tg(α + π ) = tgα oraz tg (π2-+ α) = − ctgα ).

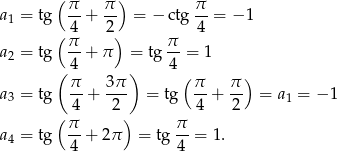
( π π ) π a1 = tg --+ -- = − ctg-- = −1 ( 4 2) 4 a2 = tg π-+ π = tg π-= 1 ( 4 ) 4 π- 3-π (π- π-) a3 = tg 4 + 2 = tg 4 + 2 = a1 = − 1 ( π ) π a4 = tg --+ 2π = tg --= 1. 4 4

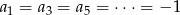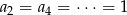itd. Widać, że a1 = a3 = a5 = ⋅⋅⋅ = − 1 i a2 = a 4 = ⋅⋅⋅ = 1 . Równości te łatwo uzasadnić (powyżej sprawdziliśmy je tylko w szczególnych przypadkach) korzystając z tego, że 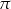π jest okresem tangensa.

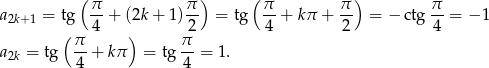
( π π ) (π π ) π a 2k+ 1 = tg --+ (2k+ 1)-- = tg -- + kπ + -- = − ctg -- = − 1 ( 4 ) 2 4 2 4 a = tg π-+ kπ = tg π- = 1. 2k 4 4

Musimy zatem policzyć sumę

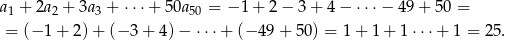
a 1 + 2a 2 + 3a 3 + ⋅⋅⋅ + 50a50 = − 1 + 2 − 3 + 4 − ⋅⋅⋅− 49+ 50 = = (−1 + 2 )+ (− 3 + 4) − ⋅⋅⋅+ (− 49+ 50) = 1 + 1 + 1 ⋅⋅⋅+ 1 = 25.

 
Odpowiedź: 25

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!