Zadanie nr 2515516

Na boku 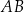trójkąta 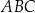ABC wybrano punkt 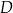w ten sposób, że 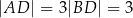|AD | = 3|BD | = 3 . Bok 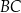tego trójkąta ma długość 2. Oblicz stosunek długości odcinków 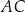i .

Wersja PDF

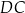Rozwiązanie

Przyjmijmy oznaczenia kątów trójkąta z poniższego rysunku.

Sposób I

Piszemy twierdzenia cosinusów w trójkątach 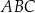ABC i DBC .

{ AC 2 = AB 2 + BC 2 − 2AB ⋅BC cosβ DC 2 = DB 2 + BC 2 − 2DB ⋅ BC cos β { AC 2 = 16 + 4 − 1 6cos β = 20 − 16 cos β 2 DC = 1 + 4 − 4 cosβ = 5 − 4co sβ.

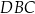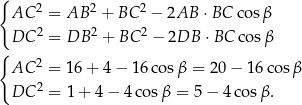
Odejmujemy teraz od pierwszej równości drugą pomnożoną przez 4.

AC 2 − 4DC 2 = 0 ⇒ AC = 2DC .

Sposób II

Piszemy twierdzenia cosinusów w trójkątach 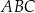ABC i ADC .

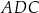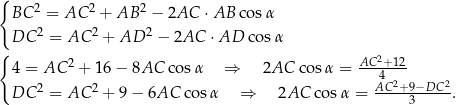
{ 2 2 2 BC = AC + AB − 2AC ⋅AB cosα DC 2 = AC 2 + AD 2 − 2AC ⋅AD cosα { 2 4 = AC 2 + 16− 8AC cosα ⇒ 2AC cosα = AC-+4-12 DC 2 = AC 2 + 9 − 6AC cos α ⇒ 2AC cos α = AC-2+9−DC-2. 3

Porównujemy teraz dwie otrzymane wartości wyrażenia 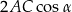2AC cosα .

AC-2-+-12- AC-2-+-9-−-DC--2 4 = 3 2 2 2 3AC + 36 = 4AC + 36 − 4DC 4DC 2 = AC 2 ⇒ AC = 2DC .

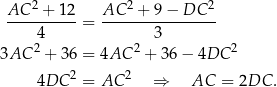
Odpowiedź: 2