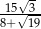/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Różne

Zadanie nr 4679316

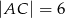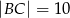W trójkącie ostrokątnym ABC dane są długości boków: |AC | = 6 , |BC | = 10 . Pole trójkąta jest równe 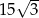√ -- 15 3 . Oblicz

  • długość boku AB ;
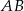  • sinus kąta BAC ;
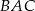  • pole koła opisanego na trójkącie ABC ;
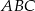  • długość promienia okręgu wpisanego w trójkąt.
Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

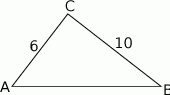
  • Mając dane dwa boki i pole możemy wyliczyć sinus kąta pomiędzy tymi bokami. To pozwoli wyliczyć 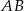AB z twierdzenia cosinusów. Liczymy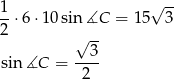
    1 √ -- --⋅6⋅ 10sin ∡C = 15 3 2 √ -- --3- sin∡C = 2

    Ponieważ trójkąt jest ostrokątny, oznacza to, że 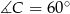∘ ∡C = 60 . Stosują twierdzenie cosinusów mamy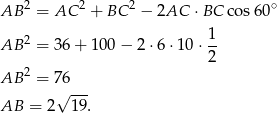

    AB 2 = AC 2 + BC 2 − 2AC ⋅BC cos60 ∘ AB 2 = 36 + 100 − 2 ⋅6 ⋅10 ⋅ 1- 2 AB 2 = 76 √ --- AB = 2 19 .

     
    Odpowiedź: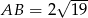 √ --- AB = 2 19

  • Liczymy jak w poprzednim podpunkcie
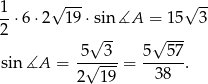
    1 √ --- √ -- -⋅6 ⋅2 1 9⋅sin ∡A = 1 5 3 2 √ -- √ --- -5--3- 5--57- sin ∡A = 2√ 19-= 38 .

    Inny sposób wyliczenia 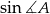sin ∡A , to skorzystanie z twierdzenia sinusów.  
    Odpowiedź: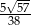 √-- 5-57- 38

  • Korzystamy z twierdzenia sinusów
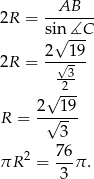
    AB 2R = ------- si√n-∡C 2--1-9 2R = √3- √ -2- 2 19 R = -√---- 3 2 76- πR = 3 π .

     
    Odpowiedź: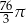 76 3-π

  • Korzystamy ze wzoru na pole
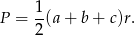
    1- P = 2 (a+ b + c)r.

    Mamy

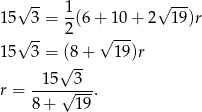
    √ -- √ --- 15 3 = 1(6 + 10 + 2 19)r √ -- 2 √ --- 15 3 = (8 + 19 )r √ -- -1-5--3-- r = √ ---. 8 + 19

     
    Odpowiedź: √ - -15√-3- 8+ 19

Wersja PDF