/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny

Zadanie nr 1075270

Dodaj do ulubionych
Dodaj do rozwiązanych

Trzy liczby o sumie 7 tworzą ciąg geometryczny. Jeżeli do drugiej liczby dodamy pierwszą to ciąg zmieni się w arytmetyczny. Wyznacz pierwszą z tych liczb. Uwzględnij wszystkie możliwości.

Rozwiązanie

Oznaczmy szukane liczby przez 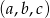(a,b ,c)

Sposób I

W ciągu geometrycznym kwadrat środkowego wyrazu jest iloczynem wyrazów sąsiednich, a w ciągu arytmetycznym wyraz środkowy jest średnią arytmetyczną wyrazów sąsiednich. Mamy więc układ równań

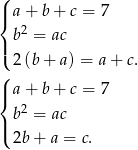
( |{ a + b + c = 7 b2 = ac |( 2 (b+ a) = a + c. (| a + b + c = 7 { b2 = ac |( 2b + a = c.

Podstawiamy 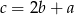c = 2b + a z trzeciego równania do dwóch pierwszych.

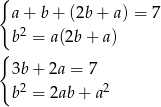
{ a+ b+ (2b+ a) = 7 b2 = a(2b + a) { 3b+ 2a = 7 b2 = 2ab + a2

Podstawiamy teraz 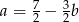7 3 a = 2 − 2b z pierwszego równania do drugiego

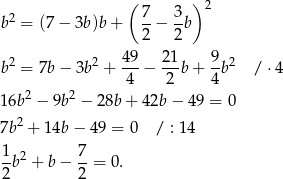
( ) 2 b2 = (7− 3b)b + 7-− 3-b 2 2 49 21 9 b2 = 7b − 3b2 + ---− --b + --b2 / ⋅4 2 2 4 2 4 16b − 9b − 28b + 42b − 49 = 0 7b2 + 14b− 49 = 0 / : 14 1-2 7- 2b + b − 2 = 0.

Rozwiązujemy otrzymane równanie kwadratowe

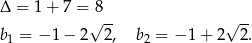
Δ = 1 + 7 = 8 √ -- √ -- b1 = − 1− 2 2, b2 = −1 + 2 2.

Mamy wtedy odpowiednio

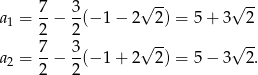
7 3 √ -- √ -- a1 = --− --(− 1 − 2 2) = 5+ 3 2 2 2 √ -- √ -- a = 7-− 3-(− 1 + 2 2) = 5− 3 2. 2 2 2

Sposób II

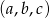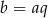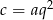Wiemy, że ciąg (a ,b ,c) jest geometryczny, więc b = aq i 2 c = aq dla pewnego 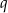q . Wiemy ponadto, że

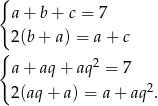
{ a+ b+ c = 7 { 2(b+ a) = a+ c a+ aq+ aq2 = 7 2 2(aq+ a) = a + aq .

Widać teraz, że drugie równanie pozwala wyliczyć 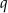q .

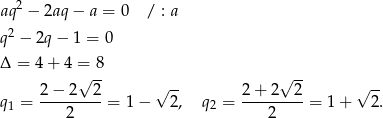
aq2 − 2aq − a = 0 / : a 2 q − 2q− 1 = 0 Δ = 4+ 4 = 8 √ -- √ -- √ -- √ -- q = 2-−-2--2-= 1 − 2, q = 2+--2--2-= 1 + 2 . 1 2 2 2

Z pierwszego równania układu obliczamy a .

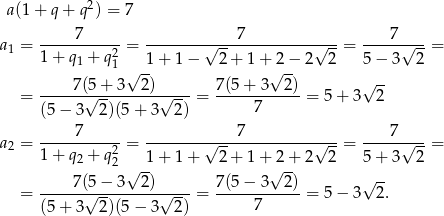
2 a(1+ q+ q ) = 7 7 7 7 a1 = ----------2 = -------√--------------√----= -----√---= 1 + q1 + q1 √ -1+ 1− 2+ 1 +√2-− 2 2 5 − 3 2 7(5+ 3 2) 7(5 + 3 2 ) √ -- = ------√---------√----= ------------= 5 + 3 2 (5 − 3 2)(5 + 3 2 ) 7 -----7----- ------------7-------------- ----7---- a2 = 1 + q + q2 = √ -- √ --= √ --= 2 2 √ -1+ 1+ 2+ 1 +√2-+ 2 2 5 + 3 2 -----7(5−--3--2)----- 7(5-−-3--2-) √ -- = √ -- √ -- = 7 = 5 − 3 2. (5 + 3 2)(5 − 3 2 )

 
Odpowiedź: 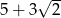√ -- 5 + 3 2 lub √ -- 5 − 3 2

Wersja PDF