/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny

Zadanie nr 1310340

Dodaj do ulubionych
Dodaj do rozwiązanych

Pierwszy wyraz ciągu arytmetycznego 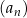(an) jest równy 2, a suma sześciu początkowych wyrazów tego ciągu wynosi 72.

  • Oblicz sumę pięćdziesięciu początkowych wyrazów tego ciągu.

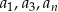  • Dla jakiego n liczby a 1,a 3,an tworzą ciąg geometryczny?

Rozwiązanie

Wiemy, że

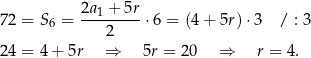
72 = S6 = 2a1 +-5r⋅ 6 = (4+ 5r)⋅3 / : 3 2 24 = 4 + 5r ⇒ 5r = 2 0 ⇒ r = 4.

  • Liczymy

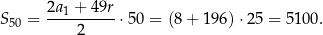
    2a + 49r S50 = --1-------⋅50 = (8+ 196)⋅ 25 = 510 0. 2

     
    Odpowiedź: 5100

  • Trzy liczby tworzą ciąg geometryczny jeżeli kwadrat środkowej z nich jest iloczynem pozostałych dwóch. Musimy więc rozwiązać równanie

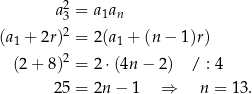
    a2 = a a 3 1 n (a 1 + 2r)2 = 2(a1 + (n − 1)r) 2 (2 + 8) = 2⋅(4n − 2) / : 4 25 = 2n− 1 ⇒ n = 13.

     
    Odpowiedź: n = 13

Wersja PDF