Definicja Ciąg 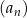 nazywamy arytmetycznym jeżeli różnica każdych dwóch jego kolejnych wyrazów jest stała (nie zależy od
nazywamy arytmetycznym jeżeli różnica każdych dwóch jego kolejnych wyrazów jest stała (nie zależy od  ).
).
W języku wzorów piszemy, że istnieje liczba  , dla której
, dla której
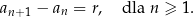
Liczbę  nazywamy różnicą ciągu
nazywamy różnicą ciągu 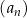 .
.
Ciąg stały
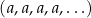
jest ciągiem arytmetycznym o różnicy 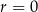 .
.
Ciąg kolejnych liczb naturalnych jest ciągiem arytmetycznym o różnicy 1.
Ciąg parzystych liczb naturalnych jest ciągiem arytmetycznym o różnicy 2.
Ciągi skończone
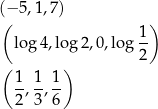
są arytmetyczne (z różnicami 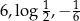 odpowiednio).
odpowiednio).
Ciągi
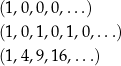
nie są arytmetyczne, bo różnica kolejnych wyrazów zależy od tego, które wyrazy od siebie odejmujemy (nie jest stała).
Dlaczego arytmetyczny? Dlaczego ciąg o stałych różnicach kolejnych wyrazów nazywamy ciągiem arytmetycznym? Powodem jest bardzo użyteczna charakteryzacja takiego ciągu:
Ciąg jest ciągiem arytmetycznym wtedy i tylko wtedy, gdy każdy wyraz, z wyjątkiem pierwszego (i ostatniego jeżeli ciąg jest skończony) jest średnią arytmetyczną wyrazów sąsiednich.
W języku wzorów piszemy, że
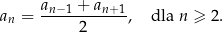
Wykluczenie z powyższego warunku wyrazów pierwszego i ostatniego powinno być oczywiste – każdy z tych wyrazów ma tylko jednego sąsiada.
Ciąg 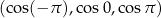 nie jest arytmetyczny, bo
nie jest arytmetyczny, bo
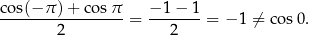
Aby sprawdzić, czy ciąg
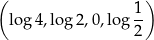
jest ciągiem arytmetycznym wystarczy sprawdzić prawdziwość dwóch równości
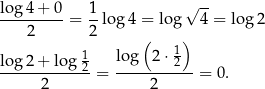
Wzory Jeżeli zapiszemy definicję ciągu arytmetycznego w postaci
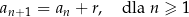
to widać, że w ciągu arytmetycznym każdy kolejny wyraz powstaje z poprzedniego przez dodanie liczby  . To oznacza, że cały ciąg jest wyznaczony przez swój pierwszy wyraz
. To oznacza, że cały ciąg jest wyznaczony przez swój pierwszy wyraz 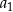 oraz różnicę
oraz różnicę  . Można to nawet powiedzieć dokładniej,
. Można to nawet powiedzieć dokładniej,  -ty wyraz powstaje z pierwszego przez dodanie
-ty wyraz powstaje z pierwszego przez dodanie 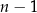 razy różnicy
razy różnicy  (bo drugi powstaje przez dodanie raz
(bo drugi powstaje przez dodanie raz  , trzeci przez dodanie dwa razy itd.). Daje to nam wzór na
, trzeci przez dodanie dwa razy itd.). Daje to nam wzór na  -ty wyraz ciągu arytmetycznego.
-ty wyraz ciągu arytmetycznego.
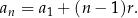
Ile jest równa 137 parzysta liczba trzycyfrowa?
Trzycyfrowe liczby parzyste tworzą ciąg arytmetyczny 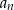 , w którym
, w którym 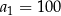 i
i 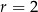 . Zatem
. Zatem
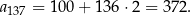
Wiedząc, że 15 wyraz ciągu arytmetycznego o różnicy -3 jest równy 77, obliczmy pierwszy wyraz tego ciągu. Liczymy
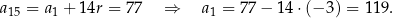
Jest jeszcze jeden wzór do zapamiętania, mianowicie wzór na sumę  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego
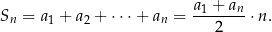
Jeżeli podstawimy w tym wzorze 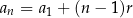 , otrzymamy drugą wersję tego wzoru
, otrzymamy drugą wersję tego wzoru
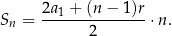
Obliczmy sumę 20 kolejnych liczb nieparzystych
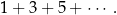
Mamy do czynienia z ciągiem arytmetycznym, w którym 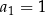 i
i 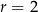 . Stosujemy zatem drugi z wzorów aby obliczyć sumę 20 początkowych wyrazów tego ciągu.
. Stosujemy zatem drugi z wzorów aby obliczyć sumę 20 początkowych wyrazów tego ciągu.
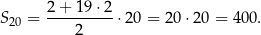
Zauważmy, że policzyliśmy tę sumę pomimo, że nawet nie wiemy ile jest równy 20 wyraz tego ciągu! Oczywiście możemy go wyliczyć
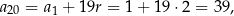
ale do policzenia sumy nie był on nam potrzebny.
Monotoniczność Dość oczywista własność, ale wyraźnie to napiszmy, bo czasem pojawia się w sformułowaniach zadań. Niech 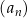 będzie ciągiem arytmetycznym o różnicy
będzie ciągiem arytmetycznym o różnicy  . Wtedy
. Wtedy
-
ciąg
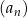 jest rosnący wtedy i tylko wtedy, gdy
jest rosnący wtedy i tylko wtedy, gdy 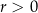 ;
; -
ciąg
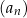 jest malejący wtedy i tylko wtedy, gdy
jest malejący wtedy i tylko wtedy, gdy 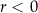 ;
; -
ciąg
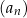 jest stały wtedy i tylko wtedy, gdy
jest stały wtedy i tylko wtedy, gdy 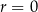 .
.
Sprawdźmy dla jakich wartości parametru 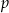 ciąg
ciąg 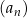 dany wzorem
dany wzorem 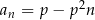 jest malejącym ciągiem arytmetycznym.
jest malejącym ciągiem arytmetycznym.
Zacznijmy od sprawdzenia, kiedy ciąg 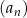 jest ciągiem arytmetycznym. Liczymy różnicę kolejnych wyrazów
jest ciągiem arytmetycznym. Liczymy różnicę kolejnych wyrazów
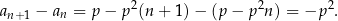
Skoro różnica nie zależy od  (jest stała), więc dla każdej wartości
(jest stała), więc dla każdej wartości 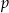 mamy do czynienia z ciągiem arytmetycznym. Ciąg ten będzie malejący o ile
mamy do czynienia z ciągiem arytmetycznym. Ciąg ten będzie malejący o ile 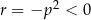 , czyli dla
, czyli dla 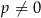 .
.

