/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny

Zadanie nr 3544779

Trzy liczby tworzą ciąg arytmetyczny. Jeśli do pierwszej z nich dodamy 5, do drugiej 3, a do trzeciej 4, to otrzymamy rosnący ciąg geometryczny, w którym trzeci wyraz jest cztery razy większy od pierwszego. Znajdź te liczby.

Wersja PDF

Rozwiązanie

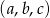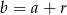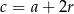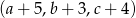Oznaczmy szukane liczby przez (a,b,c) . Wiemy, że b = a+ r i c = a+ 2r dla pewnej liczby r . Ponadto ciąg (a+ 5,b+ 3,c+ 4) jest geometryczny oraz

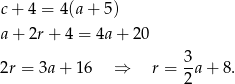
c+ 4 = 4(a + 5) a+ 2r+ 4 = 4a + 20 2r = 3a + 16 ⇒ r = 3a + 8. 2

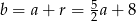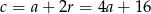Zatem b = a + r = 52 a+ 8 i c = a+ 2r = 4a + 16 .

Pozostało wykorzystać informację o ciągu geometrycznym.

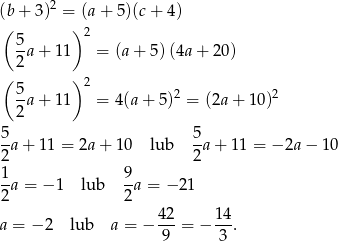
(b+ 3)2 = (a+ 5)(c+ 4) ( )2 5a + 1 1 = (a+ 5 )(4a + 20) 2 ( )2 5a + 1 1 = 4(a+ 5)2 = (2a + 10)2 2 5 5 -a + 11 = 2a+ 10 lub --a+ 1 1 = − 2a − 10 2 2 1a = − 1 lub 9a = − 2 1 2 2 4-2 14- a = − 2 lub a = − 9 = − 3 .

Otrzymujemy zatem dwa ciągi

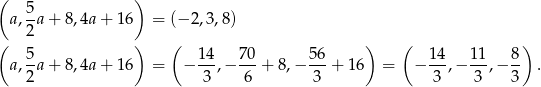
( 5 ) a,--a+ 8,4a+ 16 = (− 2,3,8) ( 2 ) ( ) ( ) 5- 14- 70- 56- 14- 11- 8- a,2 a+ 8,4a+ 16 = − 3 ,− 6 + 8,− 3 + 16 = − 3 ,− 3 ,− 3 .

Odpowiadające ciągi geometryczne to

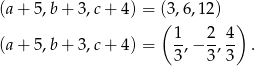
(a + 5,b + 3,c + 4) = (3 ,6,12) ( 1 2 4 ) (a + 5,b + 3,c + 4) = --,− -,-- . 3 3 3

Tylko pierwszy z tych ciągów jest rosnący, więc drugie rozwiązanie musimy odrzucić.  
Odpowiedź: (− 2,3,8)

Wersja PDF