/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny

Zadanie nr 4110660

Dodaj do ulubionych
Dodaj do rozwiązanych

Trzy liczby dodatnie tworzą ciąg arytmetyczny. Średnia arytmetyczna tych liczb jest równa 8. Jeśli od pierwszej odejmiemy 1, drugą pozostawimy bez zmian, a do trzeciej dodamy 5, to otrzymamy ciąg geometryczny. Wyznacz te liczby.

Rozwiązanie

Oznaczmy szukane liczby przez 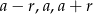a − r,a,a + r . Wtedy z podanej średniej mamy

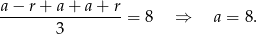
a− r + a + a + r -----------------= 8 ⇒ a = 8. 3

Zatem szukamy liczb postaci 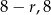8− r,8 i 8+ r .

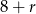Wiemy ponadto, że liczby 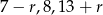7 − r,8,1 3+ r są kolejnymi wyrazami ciągu geometrycznego, czyli

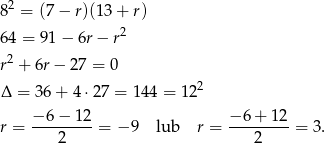
2 8 = (7 − r)(13 + r) 2 64 = 91 − 6r − r r2 + 6r − 27 = 0 2 Δ = 36+ 4⋅2 7 = 144 = 1 2 − 6 − 12 − 6+ 12 r = ---------= − 9 lub r = ---------= 3 . 2 2

Dla 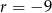r = − 9 otrzymany ciąg miałby wyrazy ujemne, więc 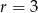r = 3 . Mamy wtedy ciąg

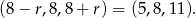
(8 − r,8,8 + r) = (5 ,8,11).

 
Odpowiedź: (5,8,11 )

Wersja PDF