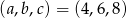/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny

Zadanie nr 5542731

Dodaj do ulubionych
Dodaj do rozwiązanych

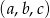Ciąg (a ,b,c) jest ciągiem arytmetycznym. Suma jego wyrazów jest równa 18. Jeżeli pierwszą z liczb zmniejszymy o 25%, a trzecią zwiększymy o 50%, to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz liczby a,b,c .

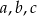Rozwiązanie

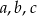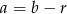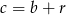Ponieważ a,b,c tworzą ciąg arytmetyczny, więc a = b − r i c = b + r dla pewnego r . Z podanej sumy mamy więc

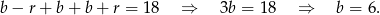
b − r+ b+ b+ r = 18 ⇒ 3b = 1 8 ⇒ b = 6.

Szukamy zatem liczb postaci 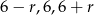6− r,6 ,6+ r . Liczby

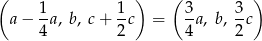
( ) ( ) a − 1-a, b , c + 1c = 3-a, b, 3-c 4 2 4 2

tworzą ciąg geometryczny, więc

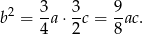
b2 = 3a ⋅ 3c = 9ac. 4 2 8

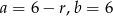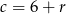Podstawiamy a = 6− r,b = 6 i c = 6 + r i mamy Podstawiamy wcześniej uzyskane wyniki i otrzymujemy

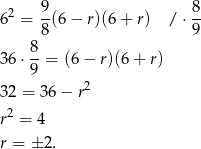
62 = 9(6 − r)(6 + r) / ⋅ 8 8 9 8- 36 ⋅9 = (6− r)(6+ r) 2 32 = 36− r r2 = 4 r = ± 2.

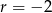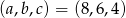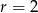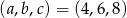Dla r = − 2 otrzymujemy ciąg (a,b,c) = (8,6,4 ) , a dla r = 2 ciąg (a,b,c) = (4 ,6,8) .  
Odpowiedź: 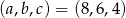(a,b,c) = (8 ,6,4) lub (a,b,c) = (4 ,6,8)

Wersja PDF