/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny

Zadanie nr 5615005

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że trójkąt, którego długości boków są trzema kolejnymi wyrazami ciągu geometrycznego, miary kątów zaś trzema kolejnymi wyrazami ciągu arytmetycznego jest trójkątem równobocznym.

Rozwiązanie

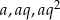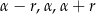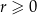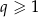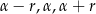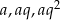Oznaczmy długości boków trójkąta przez 2 a,aq,aq , a miary kątów przez α − r,α,α + r , gdzie r ≥ 0 i q ≥ 1 . Korzystając z tego, że w trójkącie naprzeciwko większego kąta leży dłuższy bok, kąty α − r,α ,α+ r leżą naprzeciwko odpowiednio boków a,aq,aq 2 .

PIC

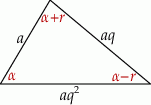
Ponieważ suma kątów w trójkącie wynosi 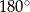18 0∘ mamy

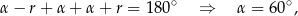
α − r+ α + α + r = 180∘ ⇒ α = 60∘,

czyli kąty mają miary 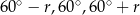60 ∘ − r,60 ∘,60∘ + r . Piszemy teraz twierdzenie cosinusów dla kąta 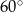60∘ i obliczamy q .

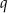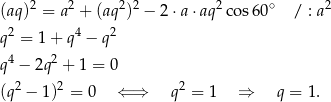
(aq)2 = a 2 + (aq2)2 − 2 ⋅a⋅ aq2cos 60∘ / : a2 2 4 2 q = 1 + q − q q4 − 2q2 + 1 = 0 2 2 2 (q − 1) = 0 ⇐ ⇒ q = 1 ⇒ q = 1 .

Zatem trójkąt jest równoboczny.

Wersja PDF