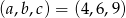Zadanie nr 7211026
Ciągi 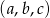 i
i 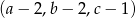 są ciągami geometrycznymi o wyrazach dodatnich, a ciąg
są ciągami geometrycznymi o wyrazach dodatnich, a ciąg 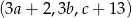 jest ciągiem arytmetycznym. Wyznacz
jest ciągiem arytmetycznym. Wyznacz 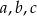 .
.
Rozwiązanie
W ciągu geometrycznym kwadrat środkowego wyrazu jest iloczynem wyrazów sąsiednich, a w ciągu arytmetycznym wyraz środkowy jest średnią arytmetyczną wyrazów sąsiednich. Mamy więc układ równań.
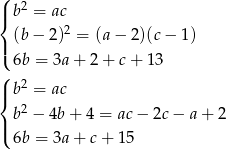
Przekształćmy drugie równanie podstawiając 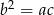 z pierwszej równości.
z pierwszej równości.
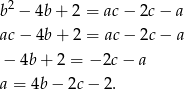
Podstawiamy teraz otrzymane wyrażenie na  do pierwszego i trzeciego równania układu - otrzymamy w ten sposób układ, w którym będą już tylko dwie niewiadome.
do pierwszego i trzeciego równania układu - otrzymamy w ten sposób układ, w którym będą już tylko dwie niewiadome.
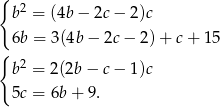
Podstawiamy teraz 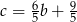 z drugiego równania do pierwszego.
z drugiego równania do pierwszego.
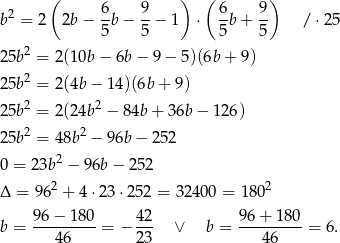
Ponieważ ciąg ma  ma mieć wyrazy dodatnie, mamy
ma mieć wyrazy dodatnie, mamy 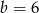 . Stąd
. Stąd
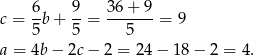
Zatem 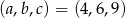 .
.
Odpowiedź: