/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny

Zadanie nr 8431477

Dodaj do ulubionych
Dodaj do rozwiązanych

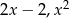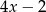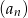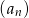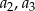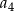Liczby 2 2x− 2,x i 4x − 2 tworzą (w podanej kolejności) ciąg arytmetyczny i są trzema początkowymi wyrazami czterowyrazowego ciągu (an) . Oblicz czwarty wyraz ciągu (an) , wiedząc że liczby a2,a3 i a4 są trzema kolejnymi wyrazami pewnego ciągu geometrycznego.

Rozwiązanie

Skoro podane liczby są kolejnymi wyrazami ciągu arytmetycznego to

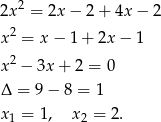
2 2x = 2x − 2+ 4x− 2 x2 = x − 1 + 2x − 1 x2 − 3x + 2 = 0 Δ = 9− 8 = 1 x1 = 1, x2 = 2.

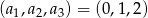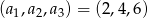Zatem mamy (a1,a2,a3) = (0,1,2) lub (a1,a2,a3) = (2,4,6 ) . Daje to nam odpowiednio

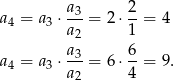
a3- 2- a4 = a3 ⋅a2 = 2⋅ 1 = 4 a 6 a4 = a3 ⋅-3-= 6⋅ --= 9. a2 4

 
Odpowiedź: 4 lub 9

Wersja PDF