/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny

Zadanie nr 9146245

Pierwszy, trzeci i trzynasty wyraz ciągu arytmetycznego 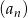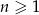(an) , n ≥ 1 są kolejnymi wyrazami ciągu geometrycznego. Piąty wyraz ciągu 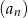(an) jest równy 27. Wyznacz wzór ciągu 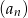(an) wiedząc, że nie jest to ciąg stały.

Wersja PDF

Rozwiązanie

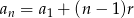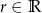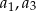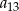Wiemy, że an = a1 + (n− 1)r dla pewnej liczby r ∈ R . Wiemy też, że liczby a1,a3 i a13 są kolejnymi wyrazami ciągu geometrycznego, więc

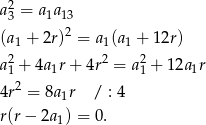
a23 = a1a13 2 (a1 + 2r) = a1(a1 + 12r) a21 + 4a1r+ 4r2 = a21 + 12a1r 2 4r = 8a1r / : 4 r(r− 2a1) = 0.

Ponieważ z założenia ciąg 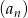(a ) n nie jest stały, mamy stąd 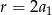r = 2a 1 . Pozostało skorzystać z warunku 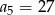a5 = 2 7 . Mamy zatem

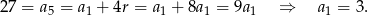
27 = a5 = a 1 + 4r = a1 + 8a 1 = 9a1 ⇒ a1 = 3 .

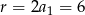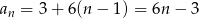Stąd r = 2a1 = 6 i an = 3+ 6(n − 1) = 6n − 3 .  
Odpowiedź: 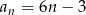an = 6n − 3 dla n ≥ 1

Wersja PDF