/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny

Zadanie nr 9792910

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma trzech liczb będących kolejnymi wyrazami rosnącego ciągu geometrycznego jest równa 52. Jeżeli do pierwszej liczby dodamy 2, do drugiej 12, a do trzeciej 6, to otrzymamy trzy kolejne wyrazy ciągu arytmetycznego. Wyznacz ten ciąg.

Rozwiązanie

Sposób I

Skoro liczby tworzą ciąg geometryczny to są postaci 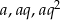2 a,aq,aq . Z podanej sumy mamy

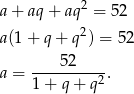
2 a+ aq+ aq = 52 a(1+ q+ q2) = 52 a = ----52----. 1 + q + q2

Z informacji o ciągu arytmetycznym wiemy, że liczby

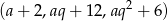
(a + 2,aq + 12 ,aq2 + 6)

są kolejnymi wyrazami ciągu arytmetycznego. Mamy zatem

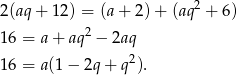
2(aq + 12) = (a + 2) + (aq2 + 6) 2 16 = a + aq − 2aq 16 = a(1 − 2q + q2).

Podstawiamy teraz 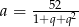---52--- a = 1+q +q2 .

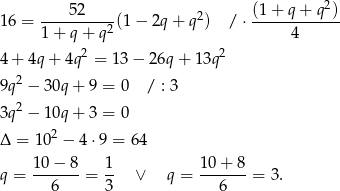
52 (1 + q + q2) 16 = ---------- (1− 2q + q2) / ⋅------------ 1 + q + q2 4 4+ 4q+ 4q2 = 13 − 26q + 1 3q2 9q2 − 30q + 9 = 0 / : 3 2 3q − 10q + 3 = 0 Δ = 1 02 − 4⋅9 = 64 q = 10-−-8-= 1- ∨ q = 10-+-8-= 3. 6 3 6

Ponieważ ciąg ma być rosnący, mamy 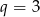q = 3 i wtedy

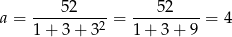
5 2 52 a = ----------= ----------= 4 1+ 3+ 32 1 + 3 + 9

i otrzymujemy ciąg 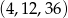(4,12,36 ) .

Sposób II

Liczby 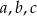a,b,c są kolejnymi wyrazami ciągu geometrycznego, czyli 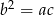b 2 = ac . Wiemy ponadto, że

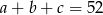
a+ b+ c = 52

oraz liczby 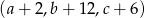(a + 2,b + 12 ,c + 6) są kolejnymi wyrazami ciągu arytmetycznego, czyli

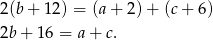
2 (b+ 1 2) = (a+ 2)+ (c+ 6 ) 2b + 1 6 = a+ c.

Podstawiając 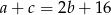a+ c = 2b+ 16 w równości 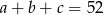a + b + c = 52 mamy

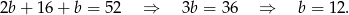
2b + 16 + b = 5 2 ⇒ 3b = 36 ⇒ b = 12.

Zatem

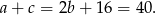
a + c = 2b + 1 6 = 40.

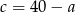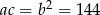Podstawiamy teraz c = 40 − a do równości ac = b 2 = 144 .

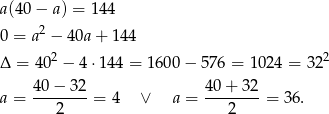
a (4 0− a) = 144 0 = a2 − 40a+ 144 Δ = 402 − 4 ⋅144 = 1600 − 576 = 1024 = 32 2 40 − 32 4 0+ 32 a = --------= 4 ∨ a = -------- = 36 . 2 2

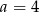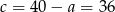Ponieważ ciąg ma być rosnący musi być a = 4 i mamy wtedy c = 40− a = 36 .  
Odpowiedź: (4,12,3 6)

Wersja PDF